antioch-0.4.0
List of all members | Public Member Functions | Private Member Functions | Private Attributes
Antioch::TroeFalloff< CoeffType > Class Template Reference

The Troe falloff model is defined by:

\[ \log_{10}\left(F\right) = \frac{\log_{10}\left(F_{\text{cent}}\right)} {1 + \left[ \frac{\log_{10}\left(P_r\right) + c} {n - d \cdot \left[\log_{10}\left(P_r\right) + c\right]} \right]^2} \]

with

\[ \begin{split} P_r & = [\mathrm{M}] \frac{k_0}{k_\infty} \\ n & = 0.75 - 1.27 \log_{10}\left(F_{\text{cent}}\right) \\ c & = - 0.40 - 0.67 \log_{10}\left(F_{\text{cent}}\right) \\ d & = 0.14 \\ F_{\text{cent}} & = (1 - \alpha) \cdot \exp\left(-\frac{T}{T^{***}}\right) + \alpha \cdot \exp\left(-\frac{T}{T^*}\right) + \exp\left(-\frac{T^{**}}{T}\right) \end{split} \]

The derivatives are therefore:

\[ \begin{split} \frac{\partial F_{\text{cent}}}{\partial T} & = \frac{\alpha - 1}{T^{***}} \cdot \exp\left(-\frac{T}{T^{***}}\right) - \frac{\alpha}{T^{*}} \cdot \exp\left(-\frac{T}{T^*}\right) + \frac{T^{**}}{T^{2}} \exp\left(-\frac{T^{**}}{T}\right) \\ \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} & = \frac{1}{\ln(10) F_\text{cent}}\frac{\partial F_\text{cent}}{\partial T} \\ \frac{\partial n}{\partial T} & = - 1.27 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\ \frac{\partial c}{\partial T} & = - 0.67 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\\\ \frac{\partial P_r}{\partial T} & = P_r \left(\frac{\partial k_0}{\partial T} \frac{1}{k_0} - \frac{\partial k_\infty}{\partial T} \frac{1}{k_\infty} \right)\\ \frac{\partial \log_{10}(P_r)}{\partial T} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial T} \\\\ \frac{\partial \log_{10}(F)}{\partial T} & = \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)}\right]^2} - \log_{10}\left(F_\text{cent}\right) 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{\left[1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2 \right]^2} \\ & = \log_{10}\left(F\right) \left[\frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{F_\text{cent}} - 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2} \right] \\ \frac{\partial F}{\partial T} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial T} \\\\\\\\ \frac{\partial P_r}{\partial c_i} & = \frac{k_0}{k_\infty} \\ \frac{\partial \log_{10}(P_r)}{\partial c_i} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial c_i} = \frac{1}{\ln(10) [\mathrm{M}]}\\\\ \frac{\partial \log_{10}\left(F\right)}{\partial c_i} & = -\frac{\log_{10}^2\left(F\right)}{\log_{10}\left(F_\text{cent}\right)} \frac{\partial \log_{10}\left(P_r\right)}{\partial c_i} \left(1 - \frac{1}{n - d\left[\log_{10}\left(P_r\right) + c\right]}\right) \left(\log_{10}\left(P_r\right) + c\right) \\ \frac{\partial F}{\partial c_i} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial c_i} \end{split} \]

. More...

#include <reaction.h>

Public Member Functions

 TroeFalloff (const unsigned int nspec, const CoeffType alpha=0, const CoeffType T3=0, const CoeffType T1=0, const CoeffType T2=1e50)
 
 ~TroeFalloff ()
 
void set_alpha (const CoeffType &al)
 
void set_T1 (const CoeffType &T)
 
void set_T2 (const CoeffType &T)
 
void set_T3 (const CoeffType &T)
 
CoeffType get_alpha () const
 
CoeffType get_T1 () const
 
CoeffType get_T2 () const
 
CoeffType get_T3 () const
 
template<typename StateType >
StateType operator() (const StateType &T, const StateType &M, const StateType &k0, const StateType &kinf) const
 
template<typename StateType , typename VectorStateType >
void F_and_derivatives (const StateType &T, const StateType &M, const StateType &k0, const StateType &dk0_dT, const StateType &kinf, const StateType &dkinf_dT, StateType &F, StateType &dF_dT, VectorStateType &dF_dX) const
 

Private Member Functions

template<typename StateType >
StateType Fcent (const StateType &T) const
 
template<typename StateType >
void Fcent_and_derivatives (const StateType &T, StateType &Fc, StateType &dFc_dT) const
 

Private Attributes

unsigned int n_spec
 
CoeffType _alpha
 
CoeffType _T3
 
CoeffType _T1
 
CoeffType _T2
 
CoeffType _c_coeff
 Precompute coefficient for log conversion. More...
 
CoeffType _n_coeff
 Precompute coefficient for log conversion. More...
 

Detailed Description

template<typename CoeffType = double>
class Antioch::TroeFalloff< CoeffType >

The Troe falloff model is defined by:

\[ \log_{10}\left(F\right) = \frac{\log_{10}\left(F_{\text{cent}}\right)} {1 + \left[ \frac{\log_{10}\left(P_r\right) + c} {n - d \cdot \left[\log_{10}\left(P_r\right) + c\right]} \right]^2} \]

with

\[ \begin{split} P_r & = [\mathrm{M}] \frac{k_0}{k_\infty} \\ n & = 0.75 - 1.27 \log_{10}\left(F_{\text{cent}}\right) \\ c & = - 0.40 - 0.67 \log_{10}\left(F_{\text{cent}}\right) \\ d & = 0.14 \\ F_{\text{cent}} & = (1 - \alpha) \cdot \exp\left(-\frac{T}{T^{***}}\right) + \alpha \cdot \exp\left(-\frac{T}{T^*}\right) + \exp\left(-\frac{T^{**}}{T}\right) \end{split} \]

The derivatives are therefore:

\[ \begin{split} \frac{\partial F_{\text{cent}}}{\partial T} & = \frac{\alpha - 1}{T^{***}} \cdot \exp\left(-\frac{T}{T^{***}}\right) - \frac{\alpha}{T^{*}} \cdot \exp\left(-\frac{T}{T^*}\right) + \frac{T^{**}}{T^{2}} \exp\left(-\frac{T^{**}}{T}\right) \\ \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} & = \frac{1}{\ln(10) F_\text{cent}}\frac{\partial F_\text{cent}}{\partial T} \\ \frac{\partial n}{\partial T} & = - 1.27 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\ \frac{\partial c}{\partial T} & = - 0.67 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\\\ \frac{\partial P_r}{\partial T} & = P_r \left(\frac{\partial k_0}{\partial T} \frac{1}{k_0} - \frac{\partial k_\infty}{\partial T} \frac{1}{k_\infty} \right)\\ \frac{\partial \log_{10}(P_r)}{\partial T} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial T} \\\\ \frac{\partial \log_{10}(F)}{\partial T} & = \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)}\right]^2} - \log_{10}\left(F_\text{cent}\right) 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{\left[1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2 \right]^2} \\ & = \log_{10}\left(F\right) \left[\frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{F_\text{cent}} - 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2} \right] \\ \frac{\partial F}{\partial T} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial T} \\\\\\\\ \frac{\partial P_r}{\partial c_i} & = \frac{k_0}{k_\infty} \\ \frac{\partial \log_{10}(P_r)}{\partial c_i} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial c_i} = \frac{1}{\ln(10) [\mathrm{M}]}\\\\ \frac{\partial \log_{10}\left(F\right)}{\partial c_i} & = -\frac{\log_{10}^2\left(F\right)}{\log_{10}\left(F_\text{cent}\right)} \frac{\partial \log_{10}\left(P_r\right)}{\partial c_i} \left(1 - \frac{1}{n - d\left[\log_{10}\left(P_r\right) + c\right]}\right) \left(\log_{10}\left(P_r\right) + c\right) \\ \frac{\partial F}{\partial c_i} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial c_i} \end{split} \]

.

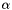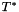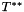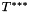$\alpha$, $T^{*}$, $T^{**}$, $T^{***}$ being the parameters of the falloff.

Definition at line 76 of file reaction.h.

Constructor & Destructor Documentation

template<typename CoeffType >
Antioch::TroeFalloff< CoeffType >::TroeFalloff ( const unsigned int  nspec,
const CoeffType  alpha = 0,
const CoeffType  T3 = 0,
const CoeffType  T1 = 0,
const CoeffType  T2 = 1e50 
)
inline

Definition at line 369 of file troe_falloff.h.

370  :
371  n_spec(nspec),
372  _alpha(alpha),
373  _T3(T3),
374  _T1(T1),
375  _T2(T2),
376  _c_coeff( CoeffType(0.67L) * Constants::log10_to_log<CoeffType>() ),
377  _n_coeff( CoeffType(1.27L) * Constants::log10_to_log<CoeffType>() )
378  {
379  return;
380  }
Antioch::TroeFalloff::_n_coeff
CoeffType _n_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:160
Antioch::TroeFalloff::_c_coeff
CoeffType _c_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:156
Antioch::TroeFalloff::n_spec
unsigned int n_spec
Definition: troe_falloff.h:148
template<typename CoeffType >
Antioch::TroeFalloff< CoeffType >::~TroeFalloff ( )
inline

Definition at line 384 of file troe_falloff.h.

385  {
386  return;
387  }

Member Function Documentation

template<typename CoeffType >
template<typename StateType , typename VectorStateType >
void Antioch::TroeFalloff< CoeffType >::F_and_derivatives ( const StateType &  T,
const StateType &  M,
const StateType &  k0,
const StateType &  dk0_dT,
const StateType &  kinf,
const StateType &  dkinf_dT,
StateType &  F,
StateType &  dF_dT,
VectorStateType &  dF_dX 
) const
inline

Definition at line 303 of file troe_falloff.h.

References antioch_assert_equal_to, Antioch::ANTIOCH_AUTO(), Antioch::constant_clone(), and Antioch::zero_clone().

312  {
313 
314  antioch_assert_equal_to(dF_dX.size(),this->n_spec);
315 
316  //declarations
317  // Pr and derivatives
318  StateType Pr = M * k0/kinf;
319  StateType dPr_dT = Pr * (dk0_dT/k0 - dkinf_dT/kinf);
320  StateType log10Pr = Constants::log10_to_log<CoeffType>() * ant_log(Pr);
321  StateType dlog10Pr_dT = Constants::log10_to_log<CoeffType>()*dPr_dT/Pr;
322  VectorStateType dlog10Pr_dX = Antioch::zero_clone(dF_dX);
323  for(unsigned int ip = 0; ip < dlog10Pr_dX.size(); ip++)
324  {//dlog10Pr_dX = 1/(ln(10)*Pr) * dPr_dX
325  dlog10Pr_dX[ip] = Constants::log10_to_log<CoeffType>()/M; //dPr_dX = k0/kinf, Pr = M k0/kinf => dlog10Pr_dX = 1/(ln(10)*M)
326  }
327  // Fcent and derivatives
328  StateType Fcent = Antioch::zero_clone(T);
329  StateType dFcent_dT = Antioch::zero_clone(T);
330  this->Fcent_and_derivatives(T,Fcent,dFcent_dT);
331  StateType dlog10Fcent_dT = Constants::log10_to_log<CoeffType>()*dFcent_dT/Fcent;
332  // Compute log(Fcent) once
333  StateType logFcent = ant_log(Fcent);
334  // n and c and derivatives
335  StateType d = Antioch::constant_clone(T, CoeffType(0.14L));
336  StateType c = - CoeffType(0.4L) - _c_coeff * logFcent;
337  StateType n = CoeffType(0.75L) - _n_coeff * logFcent;
338  StateType dc_dT = - _c_coeff * dFcent_dT/Fcent;
339  ANTIOCH_AUTO(StateType) dn_dT = - _n_coeff * dFcent_dT/Fcent;
340 
341  //log10F
342  StateType logF = logFcent/(1 + ant_pow(((log10Pr + c)/(n - d*(log10Pr + c) )),2));
343  StateType dlogF_dT = logF * (dlog10Fcent_dT / Fcent
344  - 2 * ant_pow((log10Pr + c)/(n - d * (log10Pr + c)),2)
345  * ((dlog10Pr_dT + dc_dT)/(log10Pr + c) -
346  (dn_dT - d * (dlog10Pr_dT + dc_dT))/(n - d * (log10Pr + c))
347  )
348  / (1 + ant_pow((log10Pr + c)/(n - d * (log10Pr + c)),2))
349  );
350  VectorStateType dlogF_dX = Antioch::zero_clone(dF_dX);
351  for(unsigned int ip = 0; ip < dlog10Pr_dX.size(); ip++)
352  {//dlogF_dX = - logF^2/log(Fcent) * dlog10Pr_dX * (1 - 1/(n - d * (log10Pr + c))) * (log10Pr + c)
353  dlogF_dX[ip] = - ant_pow(logF,2)/logFcent * dlog10Pr_dX[ip] *(1 - 1/(n - d * (log10Pr + c))) * (log10Pr + c);
354  }
355 
356  F = ant_exp(logF);
357  dF_dT = F * dlogF_dT;
358  for(unsigned int ip = 0; ip < dlog10Pr_dX.size(); ip++)
359  {//dF_dX = F * dlogF_dX
360  dF_dX[ip] = F * dlogF_dX[ip];
361  }
362 
363  return;
364  }
Antioch::TroeFalloff::Fcent
StateType Fcent(const StateType &T) const
Definition: troe_falloff.h:270
antioch_assert_equal_to
#define antioch_assert_equal_to(expr1, expr2)
Definition: antioch_asserts.h:74
F
Scalar F(const Scalar &x)
Definition: rotational_relaxation_unit.C:40
Antioch::constant_clone
_Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > constant_clone(const _Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > &ex, const Scalar &value)
Definition: eigen_utils.h:181
Antioch::TroeFalloff::_n_coeff
CoeffType _n_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:160
Antioch::TroeFalloff::_c_coeff
CoeffType _c_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:156
Antioch::TroeFalloff::n_spec
unsigned int n_spec
Definition: troe_falloff.h:148
Antioch::ANTIOCH_AUTO
const ANTIOCH_AUTO(StateType) KineticsTheoryThermalConductivity< ThermoEvaluator
Antioch
The parameters are reduced parameters.
Definition: chemical_mixture.h:47
Antioch::zero_clone
_Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > zero_clone(const _Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > &ex)
Definition: eigen_utils.h:145
Antioch::TroeFalloff::Fcent_and_derivatives
void Fcent_and_derivatives(const StateType &T, StateType &Fc, StateType &dFc_dT) const
Definition: troe_falloff.h:284
template<typename CoeffType >
template<typename StateType >
StateType Antioch::TroeFalloff< CoeffType >::Fcent ( const StateType &  T) const
inlineprivate

Definition at line 270 of file troe_falloff.h.

271  {
272 
273  // Fcent = (1.-alpha)*exp(-T/T***) + alpha * exp(-T/T*) + exp(-T**/T)
274  StateType Fc = (1 - _alpha) * ant_exp(-T/_T3) + _alpha * ant_exp(-T/_T1);
275 
276  if(_T2 != 1e50)Fc += ant_exp(-_T2/T);
277 
278  return Fc;
279  }
template<typename CoeffType >
template<typename StateType >
void Antioch::TroeFalloff< CoeffType >::Fcent_and_derivatives ( const StateType &  T,
StateType &  Fc,
StateType &  dFc_dT 
) const
inlineprivate

Definition at line 284 of file troe_falloff.h.

285  {
286 
287  // Fcent = (1.-alpha)*exp(-T/T***) + alpha * exp(-T/T*) + exp(-T**/T)
288  Fc = (1 - _alpha) * ant_exp(-T/_T3) + _alpha * ant_exp(-T/_T1);
289  dFc_dT = (_alpha - 1)/_T3 * ant_exp(-T/_T3) - _alpha/_T1 * ant_exp(-T/_T1);
290 
291  if(_T2 != 1e50)
292  {
293  Fc += ant_exp(-_T2/T);
294  dFc_dT += _T2/(T*T) * ant_exp(-_T2/T);
295  }
296 
297  return;
298  }
template<typename CoeffType >
CoeffType Antioch::TroeFalloff< CoeffType >::get_alpha ( ) const
inline

Definition at line 206 of file troe_falloff.h.

207  {
208  return _alpha;
209  }
template<typename CoeffType >
CoeffType Antioch::TroeFalloff< CoeffType >::get_T1 ( ) const
inline

Definition at line 213 of file troe_falloff.h.

214  {
215  return _T1;
216  }
template<typename CoeffType >
CoeffType Antioch::TroeFalloff< CoeffType >::get_T2 ( ) const
inline

Definition at line 220 of file troe_falloff.h.

221  {
222  return _T2;
223  }
template<typename CoeffType >
CoeffType Antioch::TroeFalloff< CoeffType >::get_T3 ( ) const
inline

Definition at line 227 of file troe_falloff.h.

228  {
229  return _T3;
230  }
template<typename CoeffType >
template<typename StateType >
StateType Antioch::TroeFalloff< CoeffType >::operator() ( const StateType &  T,
const StateType &  M,
const StateType &  k0,
const StateType &  kinf 
) const
inline

Definition at line 236 of file troe_falloff.h.

References Antioch::ANTIOCH_AUTO(), and Antioch::constant_clone().

240  {
241 
242  //compute log(Fcent) once
243  StateType logFcent = ant_log(this->Fcent(T));
244 
245  // Pr = [M] * k0/kinf
246  ANTIOCH_AUTO(StateType) Pr = M * k0/kinf;
247  // c = -0.4 - 0.67 * log10(Fcent)
248  // Note log10(x) = (1.0/log(10))*log(x)
249  StateType c = - CoeffType(0.4L) - _c_coeff * logFcent;
250 
251  // n = 0.75 - 1.27 * log10(Fcent)
252  // Note log10(x) = (1.0/log(10))*log(x)
253  ANTIOCH_AUTO(StateType) n = CoeffType(0.75L) - _n_coeff * logFcent;
254  ANTIOCH_AUTO(StateType) d = constant_clone(T,CoeffType(0.14L));
255 
256  StateType log10Pr = Constants::log10_to_log<CoeffType>() * ant_log(Pr);
257 
258  //log10F = log10(Fcent) / [1+((log10(Pr) + c)/(n - d*(log10(Pr) + c) ))^2]
259  //logF = log(Fcent) / [1+((log10(Pr) + c)/(n - d*(log10(Pr) + c) ))^2]
260  ANTIOCH_AUTO(StateType) logF =
261  logFcent/(1 + ant_pow(((log10Pr + c)/(n - d*(log10Pr + c) )),2) );
262 
263  return ant_exp(logF);
264  }
Antioch::TroeFalloff::Fcent
StateType Fcent(const StateType &T) const
Definition: troe_falloff.h:270
Antioch::Constants::log10_to_log
CoeffType log10_to_log()
1/ln(10)
Definition: math_constants.h:41
Antioch::constant_clone
_Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > constant_clone(const _Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > &ex, const Scalar &value)
Definition: eigen_utils.h:181
Antioch::TroeFalloff::_n_coeff
CoeffType _n_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:160
Antioch::TroeFalloff::_c_coeff
CoeffType _c_coeff
Precompute coefficient for log conversion.
Definition: troe_falloff.h:156
Antioch::ANTIOCH_AUTO
const ANTIOCH_AUTO(StateType) KineticsTheoryThermalConductivity< ThermoEvaluator
template<typename CoeffType >
void Antioch::TroeFalloff< CoeffType >::set_alpha ( const CoeffType &  al)
inline

Definition at line 174 of file troe_falloff.h.

175  {
176  _alpha = al;
177  return;
178  }
template<typename CoeffType >
void Antioch::TroeFalloff< CoeffType >::set_T1 ( const CoeffType &  T)
inline

Definition at line 182 of file troe_falloff.h.

183  {
184  _T1 = T;
185  return;
186  }
template<typename CoeffType >
void Antioch::TroeFalloff< CoeffType >::set_T2 ( const CoeffType &  T)
inline

Definition at line 190 of file troe_falloff.h.

191  {
192  _T2 = T;
193  return;
194  }
template<typename CoeffType >
void Antioch::TroeFalloff< CoeffType >::set_T3 ( const CoeffType &  T)
inline

Definition at line 198 of file troe_falloff.h.

199  {
200  _T3 = T;
201  return;
202  }

Member Data Documentation

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_alpha
private

Definition at line 149 of file troe_falloff.h.

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_c_coeff
private

Precompute coefficient for log conversion.

This is needed because Eigen doesn't understand log10.

Definition at line 156 of file troe_falloff.h.

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_n_coeff
private

Precompute coefficient for log conversion.

This is needed because Eigen doesn't understand log10.

Definition at line 160 of file troe_falloff.h.

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_T1
private

Definition at line 151 of file troe_falloff.h.

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_T2
private

Definition at line 152 of file troe_falloff.h.

template<typename CoeffType = double>
CoeffType Antioch::TroeFalloff< CoeffType >::_T3
private

Definition at line 150 of file troe_falloff.h.

template<typename CoeffType = double>
unsigned int Antioch::TroeFalloff< CoeffType >::n_spec
private

Definition at line 148 of file troe_falloff.h.

The documentation for this class was generated from the following files:
Generated on Thu Jul 7 2016 11:09:50 for antioch-0.4.0 by  doxygen 1.8.8