#include "antioch/antioch_asserts.h"#include "antioch/cmath_shims.h"#include "antioch/kinetics_type.h"#include "antioch/constant_rate.h"#include "antioch/hercourtessen_rate.h"#include "antioch/berthelot_rate.h"#include "antioch/arrhenius_rate.h"#include "antioch/berthelothercourtessen_rate.h"#include "antioch/kooij_rate.h"#include "antioch/vanthoff_rate.h"#include "antioch/photochemical_rate.h"#include "antioch/reaction_enum.h"#include "antioch/chemical_mixture.h"#include "antioch/kinetics_conditions.h"#include "antioch/kinetics_parsing.h"#include <string>#include <vector>#include <iostream>#include <limits>Go to the source code of this file.
Classes | |
| class | Antioch::ElementaryReaction< CoeffType > |
| A single reaction mechanism. More... | |
| class | Antioch::DuplicateReaction< CoeffType > |
| A single reaction mechanism. More... | |
| class | Antioch::ThreeBodyReaction< CoeffType > |
| A single reaction mechanism. More... | |
| class | Antioch::FalloffReaction< CoeffType, FalloffType > |
| Base class for falloff processes. More... | |
| class | Antioch::FalloffThreeBodyReaction< CoeffType, FalloffType > |
| Base class for falloff processes coupled with efficiencies. More... | |
| class | Antioch::LindemannFalloff< CoeffType > |
Simplest falloff model ( 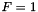 ) More... ) More... | |
| class | Antioch::TroeFalloff< CoeffType > |
| The Troe falloff model is defined by:
with
The derivatives are therefore:
. More... | |
| class | Antioch::Reaction< CoeffType, VectorCoeffType > |
| A single reaction mechanism. More... | |
Namespaces | |
| Antioch | |
| The parameters are reduced parameters. | |
![\[ \log_{10}\left(F\right) = \frac{\log_{10}\left(F_{\text{cent}}\right)} {1 + \left[ \frac{\log_{10}\left(P_r\right) + c} {n - d \cdot \left[\log_{10}\left(P_r\right) + c\right]} \right]^2} \]](form_65.png)
![\[ \begin{split} P_r & = [\mathrm{M}] \frac{k_0}{k_\infty} \\ n & = 0.75 - 1.27 \log_{10}\left(F_{\text{cent}}\right) \\ c & = - 0.40 - 0.67 \log_{10}\left(F_{\text{cent}}\right) \\ d & = 0.14 \\ F_{\text{cent}} & = (1 - \alpha) \cdot \exp\left(-\frac{T}{T^{***}}\right) + \alpha \cdot \exp\left(-\frac{T}{T^*}\right) + \exp\left(-\frac{T^{**}}{T}\right) \end{split} \]](form_66.png)
![\[ \begin{split} \frac{\partial F_{\text{cent}}}{\partial T} & = \frac{\alpha - 1}{T^{***}} \cdot \exp\left(-\frac{T}{T^{***}}\right) - \frac{\alpha}{T^{*}} \cdot \exp\left(-\frac{T}{T^*}\right) + \frac{T^{**}}{T^{2}} \exp\left(-\frac{T^{**}}{T}\right) \\ \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} & = \frac{1}{\ln(10) F_\text{cent}}\frac{\partial F_\text{cent}}{\partial T} \\ \frac{\partial n}{\partial T} & = - 1.27 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\ \frac{\partial c}{\partial T} & = - 0.67 \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \\\\ \frac{\partial P_r}{\partial T} & = P_r \left(\frac{\partial k_0}{\partial T} \frac{1}{k_0} - \frac{\partial k_\infty}{\partial T} \frac{1}{k_\infty} \right)\\ \frac{\partial \log_{10}(P_r)}{\partial T} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial T} \\\\ \frac{\partial \log_{10}(F)}{\partial T} & = \frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)}\right]^2} - \log_{10}\left(F_\text{cent}\right) 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{\left[1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2 \right]^2} \\ & = \log_{10}\left(F\right) \left[\frac{\partial \log_{10}\left(F_\text{cent}\right)}{\partial T} \frac{1}{F_\text{cent}} - 2\left[\frac{\log_{10}\left(P_r\right) + c}{n - d \left[\log_{10}\left(P_r\right) + c\right]}\right]^2 \left[\frac{\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}} {\log_{10}\left(P_r\right) + c} - \frac{\frac{\partial n}{\partial T} - d \left[\frac{\partial \log_{10}\left(P_r\right)}{\partial T} + \frac{\partial c}{\partial T}\right]} {n - d \left[\log_{10}\left(P_r\right) + c\right]} \right] \frac{1}{1 + \left[\frac{\log_{10}\left(P_r\right) + c} {n - d\left(\log_{10}\left(P_r\right) + c\right)} \right]^2} \right] \\ \frac{\partial F}{\partial T} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial T} \\\\\\\\ \frac{\partial P_r}{\partial c_i} & = \frac{k_0}{k_\infty} \\ \frac{\partial \log_{10}(P_r)}{\partial c_i} & = \frac{1}{\ln(10) P_r} \frac{\partial P_r}{\partial c_i} = \frac{1}{\ln(10) [\mathrm{M}]}\\\\ \frac{\partial \log_{10}\left(F\right)}{\partial c_i} & = -\frac{\log_{10}^2\left(F\right)}{\log_{10}\left(F_\text{cent}\right)} \frac{\partial \log_{10}\left(P_r\right)}{\partial c_i} \left(1 - \frac{1}{n - d\left[\log_{10}\left(P_r\right) + c\right]}\right) \left(\log_{10}\left(P_r\right) + c\right) \\ \frac{\partial F}{\partial c_i} & = \ln(10) F \frac{\partial \log_{10}\left(F\right)}{\partial c_i} \end{split} \]](form_67.png)